İpucu 1: Bir sayı modülü nasıl hesaplanır
İpucu 1: Bir sayı modülü nasıl hesaplanır
modül sayısı Dikey köşeli ayraçlar kullanılarak yazılmış mutlak bir değerdir: | x |. Sıfırdan herhangi bir yönde yerleştirilen aralık olarak görselleştirilebilir.

talimat
1
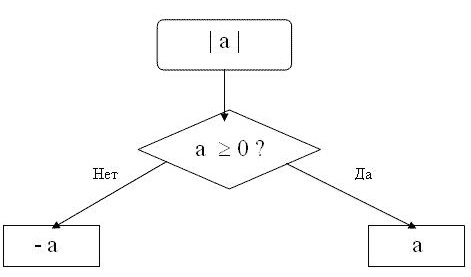
Modül sürekli olarak sunulursaişlevinde, argümanının değeri pozitif veya negatif olabilir: | x | = x, x ≥ 0; x | = - x, x <0. Sonuç olarak, parantez içinde verilen sayı herhangi bir işaret alır.
2
Sıfır modülü sıfırdır ve herhangi bir modülona olumlu bir sayı. Argüman negatifse, parantezlerin ifadesinden sonra işareti eksi ile artı arasında değişir. Buna dayanarak, karşıt sayıların modülünün | -x | 'e eşit olduğu izlenir. = | x | = x.
3
Kompleks bir sayının modülü aşağıdaki formüle göre bulunur: | a | = √b ² + c ² ve | a + b | ≤ | a | + | b | Bağımsız değişken çarpanı olarak pozitif bir tam sayı içeriyorsa, köşeli parantez işaretinin dışına çıkarılabilir, örneğin: | 4 * b | = 4 * | b |
4
Modül negatif olamaz, böylece herhangi bir negatif sayı pozitife çevrilir: | -x | = x, | -2 | = 2, | -1/7 | = 1/7, | -2.5 | = 2.5.
5
Eğer argüman karmaşık bir sayı olarak gösteriliyorsa,hesaplamaların kolay olması için, ifadenin köşeli parantez içine alınmış terimlerin sırasını değiştirmek için izin verilir: | 2-3 | = | 3-2 | = 3-2 = 1, çünkü (2-3) sıfırdan düşüktür.
6
Yükseltilmiş argüman, aynı sıranın kök işareti altında aynı zamanda - modül yardımıyla çözülür: √a² = | a | = ± a.
7
Içermeyen bir görevin varsamodülün parantezlerini genişletme koşulu, onlardan kurtulmanız gerekmez - bu sonuçtur. Ve bunları ifşa etmek istiyorsanız, işareti belirtmeniz gerekir ±. Örneğin, ifadesinin değerini bulmanız gerekir √ (2 * (4-b)) ². Çözüm şöyle görünür: √ (2 * (4-b)) ² = | 2 * (4-b) | = 2 * | 4-b | 'dir. 4-b ifadesinin işareti bilinmediğinden parantez içinde bırakılmalıdır. Ek bir koşul eklersek, örneğin, | 4-b | > 0, sonra sonuç olarak 2 * | 4-b | = 2 * (4-b). Bilinmeyen bir unsur olarak belirli bir sayı da belirtilebilir, bu nedenle belirli bir sayı dikkate alınmalıdır; ifadenin işaretini etkileyecektir.
İpucu 2: Bir sayı modülü nasıl bulunur?
modül sayısı n başlangıçtan n noktasına kadar olan birim segmentlerin sayısıdır. Ve bu mesafenin hangi yönde ölçüleceği önemli değil - sağa veya sıfıra sola.
talimat
1
modül sayısı bunun mutlak değeri de denir sayısı. Sola ve sağa çekilen kısa dikey çizgilerle gösterilir. sayısı. Örneğin, modül sayısı 15 şöyle yazılmıştır: | 15 |.
2
Bir modülün yalnızca pozitif sayı veya sıfır olabileceğini unutmayın. modül pozitif sayısı rakamın kendisine eşittir. modül Sıfır sıfıra eşittir. Yani, herhangi biri için sayısı n, sıfırdan büyük veya sıfıra eşitse, aşağıdaki formül geçerlidir: | n | = n. Örneğin, | 15 | = 15, yani modül sayısı 15 15'e eşittir.
3
Negatif sayısı aynı sayı olacak, ancak karşıt işaretle. Yani, herhangi biri için sayısı n, sıfırdan küçük ise | n | = -n. Örneğin, | -28 | = 28. modül sayısı -28 28'e eşittir.
4
Sadece tamsayılar için değil aynı zamanda kesirli rakamlar için de modülleri bulabilirsiniz. Kesirli sayılar için de aynı kurallar geçerlidir. Örneğin, 0,25 | = 25, yani modül sayısı 0,25 0,25'e eşit olacaktır. A | -2 | = ¾, yani modül sayısı -34, ¾'e eşit olacaktır.
5
Modüller ile çalışırken, karşıt sayıların modüllerinin daima birbirine eşit olduğunu bilmek önemlidir, | n | = | -n |. Modüllerin temel özelliği budur. Örneğin, | 10 | = | -10 |. modül sayısı 10, modülde olduğu gibi 10'dur sayısı -10. Buna ek olarak | a - b | = | b - a |, çünkü a noktasından b noktasına olan mesafe ve b'den a'ya olan uzaklık birbirine eşittir. Örneğin, | 25 - 5 | = | 5 - 25 |, yani | 20 | = | - 20 |.
İpucu 3: Karmaşık sayıları hesaplama
Karmaşık sayılar - kavramın daha da genişletilmesiRakamlar gerçek sayılarla karşılaştırılır. Karmaşık sayıların matematik bir giriş birçok yasa ve formüllere bitmiş bir görünüm vermek ve aynı zamanda matematik farklı alanlar arasındaki derin bağlantıları ortaya çıkarmak için yardımcı oldu.
talimat
1
Bilindiği gibi gerçek sayı yoktur.Yani b <0 ise, böyle bir bulmak mümkün değil, negatif bir sayının karekökü olabilir bir ^ 2 = b.V Bu konuda, bu böyle bir ifade edebileceği yardımıyla, yeni bir birim tanıtmak karar verildi. Buna hayali birim ve i ifadesi denir. Hayali birim, -1'in kareköküne eşittir.
2
I ^ 2 = -1 olduğundan o zaman √ (-b ^ 2) = √ ((- 1) * b ^ 2) = √ (-1) * √ (b ^ 2) = ib. Böylece, hayali bir sayı kavramı ortaya atıldı. Herhangi bir sanal sayı ib olarak ifade edilebilir, burada b gerçek bir sayıdır.
3
Gerçek sayılar formda temsil edilebilireksi sonsuzluktan artı sonsuzluğa sayısal eksen. Gerçek sayı eksenine dikey eksene benzeyen biçimde sanal rakamların temsil edilmesi elverişli idi. Birlikte, sayısal düzlemin koordinatlarını oluştururlar.Bu durumda sayısal düzlemin koordinatları (a, b) olan her noktasına a ve b'nin gerçek sayı olduğu a + ib formundaki tek ve tek bir karmaşık sayı karşılık gelir. Bu toplamın ilk terimi karmaşık sayının gerçek kısmı, ikinci terim ise hayali kısım olarak adlandırılır.
4
Eğer a = 0 ise, karmaşık sayı saf hayali olarak adlandırılır. B = 0 ise, sayı gerçek olarak adlandırılır.
5
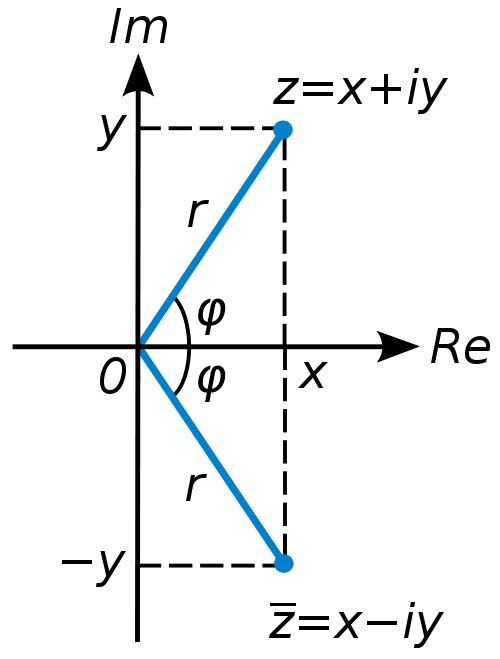
Gerçek ile hayali arasındaki ilâve işaretiKarmaşık bir sayının kısımları aritmetik toplamı göstermez. Daha ziyade, kompleks sayı olan başlangıç kökenli denk gelen bir vektör olarak temsil edilebilir, ve son nokta (a, b) bir vektör var referansla, y karmaşık sayı mutlak değeri veya modülü yer almaktadır. | Z | z = x + iy sonra ise = √ (x2 + y ^ 2).
6
İki karmaşık sayı sadece eşit olarak kabul edilirGerçek parçası ve diğeri hayali kısmına eşit gerçek bir parçası diğerinin sanal kısmı ise, yani: eşitsizlik işaretleri anlamı yok karmaşık sayılar için x1 = x2 ve y1 = y2.Odnako, o değilse z1 = z2, söylemek , öyle ki z1 <z2 veya z1> z2. Bu şekilde karmaşık sayıların modüllerini sadece karşılaştırabilirsiniz.
7
Z1 = x1 + iy1 ve z2 = x2 + iy2 kompleks isenumaraları, o zaman: z1 + z 2 = (X1 + X2) + i (y1 + y2); Z1 - Z2 = (x1 - X2) + i (y1 - y2) kompleks sayı toplama ve çıkarma aynı aşağıda olduğu kolayca Ayrıca ve vektörlerin çıkarma bertaraf ettiğini.
8
iki karmaşık sayının ürünü eşit: * (x2 + iy2) x 1 * x2 + ı * y1 * x2 + i * X1 * Y2 + (i ^ 2) * y1 * I y2.Poskolku = z1 * Z2 = (x1 + iy1) ^ 2 = -1, daha sonra, son sonucudur: (x1 * x2 - y1 * y2) + i (x1 * y2 + x2 * y1).
9
Üsselleştirme işlemleri ve kök ekstraksiyonukarmaşık sayılar için gerçek aynı şekilde tanımlanmıştır. Bununla birlikte, herhangi bir sayıda karmaşık alanı tam olarak bu sayı, b, bu b ^ n = bir, diğer bir deyişle n kökleri stepeni.V özellikle n-inci, bu n'inci derece bir cebirsel denklemler bir değişken sahip olduğu anlamına gelir tam n var içinde karmaşık kökler, bazıları geçerli olabilir.
İpucu 4: Köküne sayı ekleme
Kök belirten bir simgedirböyle bir sayının bulunması, kök işaretinden önceki dereceye kadar olan ereksiyonun bu işaret altında belirtilen numarayı vermesinin matematiksel işlemi. Çoğu zaman köklerin olduğu problemleri çözmek için yalnızca değeri hesaplamak yeterli değildir. Ek işlemler gerçekleştirmeliyiz, bunlardan biri, kök işaretine bir sayı, değişken veya ifadenin eklenmesidir.

talimat
1
Kökün üsünü belirleyin. Bir indeks, bir kök ifadesi elde etmek için kök hesabının sonucunun hangi dereceye kadar çıkması gerektiğini gösteren bir tamsayıdır (bu kökün çıkarıldığı sayı). Kökün üssü, kök sembolünün önünde bir üst indeks biçiminde yazılır. Bu indeks belirtilmemişse, derece derecesi iki olan kareköküdür. Örneğin, kök dizin √3 ikiye eşittir, dizin ³√3 üç eşittir, kök üssü √√3 dört eşittir vs.
2
Altında yapmak istediğiniz numarayı yükseltinbir kök işareti, önceki adımda sizin tarafınızdan belirlendiği üzere bu kökün üsüne eşit bir güce dönüştürür. Örneğin, kök işareti ⁴√3 altında 5 sayısını girmek istiyorsanız, kökün üssü dörttür ve 5'in dikey sonucunu dördüncü güç 5⁴ = 625 olarak hesaplamanız gerekir. Bunu, internete yerleştirilen bir hesap makinesinin veya ilgili çevrimiçi hizmetlerin yardımıyla aklınızda herhangi bir şekilde uygun bir şekilde yapabilirsiniz.
3
Önceki adımda elde edilen değeri girinradikaller ve ifadelerin çarpanları olarak kök işaretinin altında. Önceki adımda kullanılan örnek için kök ⁴√3'e 5 (5 * ⁴√3) numarasının eklenmesiyle bu eylem şu şekilde yazılabilir: 5 * ⁴√3 = ⁴√ (625 * 3).
4
Türetilmiş radikali basitleştirin, eğerbu mümkündür. Önceki adımlardan bir örnek için, bunun anlamı, yalnızca kök işareti altındaki sayıları çarpmanız gerektiğidir: 5 * ⁴√3 = ⁴√ (625 * 3) = ⁴√1875. Bu sayının kök altına girilmesi işlemini tamamlar.
5
Sorunda bilinmeyen varsadeğişkenler için yukarıda açıklanan adımlar genel bir şekilde yapılabilir. Eğer bilinmeyen değişken x'in dördüncü kök yapmak istiyorsanız Örneğin, radikal bir anlatım, eylemlerin tüm dizisi olarak yazılabilir 5 / x³ eşittir: ⁴√ x * ⁴√ (5 / x³) = (x⁴ * 5 / x³) = ⁴√ (x * 5).
İpucu 5: Karmaşık sayı modülü nasıl bulunur?
Gerçek sayılar yeterli değilherhangi bir ikinci dereceden denklemi çözebilirler. Gerçek sayılar arasında kökleri olmayan ikinci dereceden denklemlerin en basiti x ^ 2 + 1 = 0'dır. Çözürken, x = ± sqrt (-1) olduğu ortaya çıkar ve temel cebir yasalarına göre, negatiften eşit derecede bir kök çıkarılır sayısı imkansızdır.

Ihtiyacınız olacak
- - Kağıt;
- - sap.
talimat
1
Bu durumda iki yol vardır: İlk - kurulmuş yasaklar takip etmek ve bu denklem kökleri değil sahip olduğunu varsaymak; İkinci - denklem biçimi z = a + ib kavramını kornem.Tak karmaşık sayılar, sahip olacağı ölçüde gerçek sayılar Sistemi genişletmek için formül (i ^ 2) = - 1, burada i - hayali birimi. sayılar a ve b gerçek ve sanal kısımları sırasıyla denir sayısı z Rez ve Imz. Kompleks ile eylemlerde önemli rol sayısıoynuyor sayısı karmaşık eşlenik. Z = a + ib kompleks numarasına eşlenik, zs = a-ib olarak adlandırılır, yani sayının imgesel birimin önünde karşıt işaret vardır. Yani eğer z = 3 + 2i, o zaman zs = 3-2i Herhangi bir gerçek sayı bir kompleksin özel bir örneğidir sayısı, hayali kısmı sıfırdır. 0 + i0 sıfıra eşit karmaşık bir sayıdır.
2
karmaşık sayısı Bu şekilde eklenebilir ve çoğaltılabilir.cebirsel ifadelerle yapmak. Bu durumda, toplam ve çarpım olağan yasaları geçerli kalır. Z1 = A1 + IB 1, Z2 = a2 + ib2.1 olsun. Toplama ve vychitanie.z1 + z 2 = (A1 + A2) + i (b1 ve b2), Z1-Z2 = (A1-A2) + i (b1-b2). 2. Umnozhenie.z1 * Z2 = (A1 + IB1) (a2 + ^ 2) = a1a2 + ia1b2 + ia2b1 + (i ^ 2) B1B2 = (a1a2-B1B2) + i (a1b2 + a2b1) .Eğer sadece açık parantez çarpılıp tanım i ^ 2 = -1 kullanılır. Ürün eşlenik sayı gerçek bir sayıdır; z * zs = (a + IB), (a-ib) bir ^ 2- (i ^ 2), (b ^ 2) ^ 2 + b ^ = 2 ==.
3
3. Bölüm.standart forma özel z1 / z2 = (a1 + IB 1) / (a2 + ^ 2) getirmek için payda hayali birimin kurtulmak için. ((A1 + IB1), (a2-^ 2)) / ((a2 + ^ 2), (a2-^ 2)) = ((a1a2 + B1B2) + i (a2b1 Bu en kolay için konjügat payda ile Pay ve paydayı çoğalmaya -a1b2)) / (a ^ 2 + b ^ 2) = = (a1a2 + B1B2) / (a ^ 2 + b ^ 2) + i (a2b1-a1b2) / (a ^ 2 + b ^ 2) .Operatsii Çarpma ve bölünmenin yanı sıra toplama ve çıkarma karşılıklı olarak tersidir.
4
5
Kompleks düzlemin her bir noktası z ile bu noktanın yarıçap vektörü bağlanır. Z kompleks sayısını temsil eden yarıçap vektörünün uzunluğuna r = | z | modülü denir. entegre sayısı; ve gerçek eksenin pozitif yönü ile vektörün 0Z yönü arasındaki açıya bu kompleksin argz argümanı denir sayısı.
6
Bir kompleksin argümanı sayısı sayılırsa pozitif olarak kabul edilir.eksenin pozitif yönde 0x saatin tersi yönünde, negatif yönde ters yönde. Tek bir karmaşık sayı, argz + 2nk argümanının değerler kümesine karşılık gelir. Bu değerlerden, argz değerleri, -n'den n'ye uzanan aralıkta esas alınır. Konjugat kompleksi sayısı z ve zs eşit modüllere sahiptir ve argümanları mutlak değerde eşittir ancak işaret farklılık gösterir.
7
Böylece | z | ^ 2 = a ^ 2 + b ^ 2, | z | = sqrt (a ^ 2 + b ^ 2). Yani eğer z = 3-5i ise, | z | = sqrt (9 + 25) = 6 olur. Buna ek olarak, z * zs = | z | ^ 2 = a ^ 2 + b ^ 2 olduğundan, imgesel birimin tekrar tekrar ortaya çıkabileceği kompleks ifadelerin modüllerini hesaplamak mümkündür z = (1-3i) ( 4 + i) / (2-2i) = 9/2-i, modülün doğrudan bir hesabı | z | ^ 2 = 81/4 + 1 = 85/4 ve | z | = sqrt (85) / 2 verir. Hesaplama aşamasını aşarak, zs = (1 + 3i) (4-i) / (2 + 2i) dikkate alındığında şunu yazabiliriz: | z | ^ 2 = z * zs == (1-3i) (1 + 3i (4 + i) / (4 + 4) = 85/4 ve | z | = (4 + i) (4-2) sqrt (85) / 2.
İpucu 6: Bir modül nasıl eklenir?
Modül - toplamın, bütün bir şeyin ayrılmaz bir parçasıdır. Modül ana çekirdeği yok etmeden eklenebilir veya çıkarılabilir. Modül bir program olabilir, cihazın bir parçası olabilir. Benzer bir tasarım, örneğin Linux işletim sisteminde de kullanılır. Modüler mimari bir Linux çekirdeğine sahiptir.

Ihtiyacınız olacak
- - PC;
- - Linux işletim sistemi.
talimat
1
Linux işletim sisteminde modüller eklemek veya modülleri kaldırmak için özel komutlar ve modprobe programı bulunur. Linux çekirdeğinin kendisi, bir veya başka bir değeri destekleyen birçok kod içerir.
2
Tüm modüller özel bir dizinde/ lib / modules / $ (uname -r). Modprobe komutuyla Linux çekirdeğine bir modül ekleme veya modül kaldırma. Önce kullanıcı şifresini girin ve yönetici olarak oturum açın.
3
Standart komut satırı istemikod şuna benzer: [leh @ localhost leh] #. Modül ekleme komutu şu şekilde girilmelidir: sudo modprobe vboxdrv. Ardından, Linux sisteminizde gerekli modülü bulun.
4
Tüm ana modüller yüklenmelidirotomatik. Herhangi bir donanım yükledikten sonra hala bir çekirdek modülü eklemeniz gerekiyorsa, Kudzu programı başlamalıdır. Bu ekipmanın sistem tarafından desteklenip desteklenmediğini belirleyecek ve modülünü yapılandıracaktır. Modül başarıyla eklenmiş olup olmadığını öğrenmek için / sbin / lsmod komutunu kullanın.







