İpucu 1: Hız projeksiyonunu bulma
İpucu 1: Hız projeksiyonunu bulma
Hız vektörü vücudun hareketi karakterize eder,uzayın hareketinin yönünü ve hızını gösterir. Bir fonksiyon olarak hız, koordinat denkleminin birinci türevidir. Hızın türevi ivme kazandıracaktır.

talimat
1
Vektörün kendisi hiçbir şey vermezHareketin matematiksel tanımlamasının planı, dolayısıyla koordinat eksenlerindeki projeksiyonlarda düşünülür. Bir koordinat ekseni (ışın), iki (düzlem) veya üç (boşluk) olabilir. Projeksiyonları bulmak için eksendeki vektörün uçlarından dik açılı bırakmanız gerekir.
2
Projeksiyon, vektörün bir tür "gölge" si. Vücut dikkate alınan eksene dik olarak hareket ederse, projeksiyon bir noktaya kadar dejenere olur ve sıfır değeri olacaktır. Koordinat eksenine paralel hareket ederken, projeksiyon vektöre ait modül ile çakışır. Ve vücut hareket ettirildiğinde hız vektörü φ x ışını yönünde bir açıyla yönlendirilirse, x ekseni üzerindeki çıkıntı bir segment olur: V vektör hız vektörü modülüdür. V (x) = V • cos (φ). Hız vektörünün yönü koordinat ekseninin pozitif yönü ile çakıştığında yansıtma pozitiftir ve aksi durumda negatiftir.
3
Bir noktanın hareketi koordinatla verilsindenklemler: x = x (t) y y (t), z = z (t) =. Sonra üç eksenine izdüşümü fonksiyonlar hızı, forma sahip olacak, sırasıyla V (x) = dx / dt = X "(t), V (y) = dy / dt = y" (t), V (z) = dz / dt = z "(t), yani türevleri almak için gerekli hız bulmak. kendini hız vektörü denklem V = V (x) ile ifade edilecektir • i + V (y) • j + V (z) '• k, burada i , j, k -. eksenleri x, y koordinatı, z modülü hız formül V = √ hesaplanabilir birim vektörleri (V (x) ^ 2 + V (y) ^ 2 + V (z) ^ 2).
4
Hız vektörü u'nun kosinüsleri vasıtasıylakoordinat eksenlerinin tek segmanlarında vektörün yönünü belirleyebilir, modülünü atarsınız. Bir düzlemde hareket eden bir nokta için iki koordinat x ve y yeterlidir. Vücut çevre çevresinde hareket ederse, hız vektörünün yönü sürekli değişir ve modül sabit tutulabilir veya zamanla değişebilir.
İpucu 2: projeksiyon noktaları nasıl bulunur?
Nesnenin son görüntüsünü oluşturmadan önce,tüm detayları (temel bileşenler) çizmek ayrı ayrı yapılır. Herhangi bir geometrik nesne, noktadan oluşan çizgilerden, düzlemlerden oluşur. Bu makalede puanların nasıl yansıtılacağı anlatılmaktadır.

Ihtiyacınız olacak
- Kurşun kalem, cetvel, betimsel geometri veya çizim ders kitabı.
talimat
1
Projeksiyon yöntemini kullanarak,Çizimler üzerindeki geometrik cisim görüntüleri, bir resim yeterli olmazsa, cisimlerin şekillerinin net bir şekilde aktarılması için, temel geometrik bileşenleri, en az iki projeksiyon gerekir. Bu nedenle uzaydaki bir noktayı belirlemek için iki projeksiyon gereklidir.
2
Bir dihedral açı c uzayını düşününA noktası, içeridedir, projeksiyonunun yapılması gerekir. İki projeksiyon düzlemi kullanılır: yatay P1 ve dikey P2 (yatayya dikey ve izleyicinin önünde bulunur) Düşey bir düzlem üzerinde bir düzlem, çizgi veya noktanın projeksiyonlarına ön çıkıntılar denir. Projeksiyon ekseni, bir çizgi olan projeksiyon planlarının kesişimi.
3
Bir projeksiyon düzleminde, A noktasıortogonaldir. Dikey projeksiyon ışınları, çıkıntıların uçlarına dik olan bir çıkıntı yapan düzleme birleştirilir P2 / P1 ekseni boyunca dönerek yatay ve dikey düzlem P1 ve P2'yi eşleştirerek düz bir çizim elde edilir.
4
P2 / P1 eksenine dikey olarak, noktanın her iki çıkıntısının üzerine yerleştirildiği bir çizgi vardır. A1 ve A2 - noktanın yatay ve öne çıkıntıları A1A2 düz hattı - dikey bağlantı ile bağlanır.
5
Sonuç olarak, kapsamlı birburada bir noktanın izdüşüm düzlemlerine göre konumu, birbirine bağlı ortogonal projeksiyonlarla benzersiz şekilde belirlenir. Oluşturulan dikey çizgi bölümlerinden dolayı, noktanın izdüşüm düzlemlerine göre konumunu belirleyebilirsiniz.
İpucu 3: Eksen üzerindeki projeksiyonlar nasıl bulunur?
Bir vektörün veya bir parçanın koordinat üzerindeki izdüşümü bulmak için eksen, uç noktalarından eksenlere kadar dik açılılar bırakmanız gerekir. Bir vektörün veya bir bölümün koordinatları biliniyorsa, üzerine bir projektör eksen hesaplanabilir. Vektörün uzunluğu ve bununla eksen arasındaki açı biliniyorsa aynı şey yapılabilir.
Ihtiyacınız olacak
- - Kartezyen koordinat sistemi kavramı;
- - trigonometrik fonksiyonlar;
- - vektörler ile eylemler.
talimat
1
Koordinat sisteminde bir vektör veya bir segment çizin. Ardından, segmentin veya vektörün bir ucundan perdelgileri her bir eksene indirgeyin. Dikey ile her biri arasındaki kavşakta eksen noktayı işaretleyin. Bu işlemi, segmentin veya vektörün ikinci ucu için tekrarlayın.
2
Koordinatların menşei ile merkezlerin kesişme noktalarının her biri arasındaki koordinat sistemiyle mesafesini ölçün. her biri üzerinde eksen Daha büyük bir mesafeden küçük çıkartın - bu, her eksende segmentin veya vektörün izdüşümüdür.
3
Bir vektörün ya da bir segmentin bitişlerinin koordinatlarının onu bulduğu biliniyorsa projeksiyonlar Üzerinde eksen, karşılık gelen koordinatları sonun koordinatlarından çıkartınbaşın koordinatları. Değer negatifse, modülünü alın. Eksi işareti projeksiyonun koordinatın negatif parçası olduğu anlamına gelir eksen. Örneğin, vektörün orijininin koordinatları (-2; 4; 0) ve ucun koordinatları (2; 6; 4) ise OX eksenine yansıtma OY ekseni üzerinde 2 - (-2) = 4'tür: 6-4 = 2 , OZ ekseni üzerinde: 4-0 = 4.
4
Eğer vektörün koordinatları verilirse, bunlar karşılık gelen eksen. Örneğin, bir vektörün koordinatları varsa(4; -2; 5), OX ekseninin OY ekseninde OY: 2 ekseni üzerinde 4 olduğu anlamına gelir: 5. Vektörün koordinatı 0 ise, bu eksendeki yansıması da 0 olur.
5
Vektörün uzunluğu ve eksen arasındaki açı (polar koordinatlarda olduğu gibi) biliniyorsa, bu eksene yansımasını bulmak için bu vektörün uzunluğunu k ile çarpmamız gerekireksenEksen ve vektör arasındaki burun açısı. Örneğin vektörün uzunluğunun 4 cm olduğu biliniyorsa ve XOY koordinat sisteminde OX ekseni arasındaki açı 60 ° 'dur.
6
Projeksiyonunu OX ekseni üzerinde bulmak için, 4 ile çarpın.cos (60º). Hesaplama 4 • cos (60 °) = 4 • 1/2 = 2 cm. Bu vektör ve 90 °-60 ° = 30 ° arasında bir açı bularak OY ekseni üzerinde bir çıkıntı bulun. Daha sonra bu eksende çıkıntısı 4 • cos (30 °) = 4 3,46 = 0866 • cm'dir.
İpucu 4: Yön cosinelerini bulma
Matematik karmaşık ve kesin bir bilimdir. Buna yaklaşım, okur yazarlık için gereklidir, acele etmeyin. Doğal olarak, soyut düşünme olmadan yapamaz. Hesaplamaların görsel basitleştirilmesi için kağıttan oluşan bir kalem gibi.
talimat
1
Gama, beta ve alfa harfleriyle açıları not edin,bunlar koordinat ekseninin pozitif yönde bir yönü olan B vektörü tarafından oluşturulur. Bu açıların kosinüsleri, vektörün B. yön kosinüsleri olarak adlandırılmalıdır.
2
Dikdörtgen Kartezyen koordinat sistemindeB'nin koordinatları, vektörün koordinat ekseni üzerindeki projeksiyonlarına eşittir. Böylece, B1 = | B | cos (alfa), B2 = | B | cos (beta), B3 = | B | cos (gama). Bu şu şekildedir: cos (alpha) = B1 || B |, cos (beta) = B2 || B |, cos (gamma) = B3 / | B |, burada | B | = sqrt (B1 ^ 2 + B2 ^ 2 + B3 ^ 2). Ve bu cos (alfa) = B1 | sqrt (B1 ^ 2 + B2 ^ 2 + B3 ^ 2), cos (beta) = B2 | sqrt (B1 ^ 2 + B2 ^ 2 + B3 ^ 2), cos gama) = B3 / sqrt (B1 ^ 2 + B2 ^ 2 + B3 ^ 2).
3
Şimdi ana mülkü vurgulamalıyızyönlendirir. (B 1 ^ 2 + B2 ^ 2 + B3 ^ 2 | vektör kosinüs kılavuzları karelerinin toplamı her zaman ^ 2 (alfa) + cos ^ 2 (P) + cos ^ 2 (y) = B1 ^ 2 cos eşit edinitse.Pravda olacak ) + B2 ^ 2 | (B1 ^ 2 + B2 ^ 2 + B3 ^ 2) + B3 ^ 2 / (B1 ^ 2 + B2 ^ 2 + B3 ^ 2) = (B1 ^ 2 + B2 ^ 2 + B3 ^ 2 ) | (B1 ^ 2 + B2 ^ 2 + B3 ^ 2) = 1.
4
Örneğin verilen: B vektörü = {1, 3, 5). Sorunun çözümü şu şekildedir: B | = (Bx ^ 2 + By ^ 2 + Bz ^ 2) = sqrt (1 + 9 +25) = sqrt (35) = 5,91. aşağıdaki formda yazılabilir: {cos (alfa), cos (beta), cos (gamma)} = {1 / sqrt (35), 3 / sqrt (35), 5 / (35)} = {0,16; 0 , 5, 0.84}.
5
Bulmanın başka bir yolu. B vektörünün yön kosinüslerini bulmaya çalışırken, skaler ürün tekniğini kullanın. Bu vektör B ve Kartezyen Z, X ve c koordinatları yönü vektörleri arasındaki açılar gerekir. Bunların koordinatları {1, 0, 0}, {0, 1, 0}, {0, 0, 1} vektörün skaler ürünü bulmak .Þimdi: tavuk vektörleri arasındaki açı, D, modüllerinin ürüne eşit olan bir dizi iki vektörün ürünü D. cos vektörler (b, b) = | b || b | (cos | b || z | | cos (a) ya da B 1 = | B (b, z) = o, b = z ise D. cos a). Bundan başka, bütün aşamalar koordinatlar x ve c ile, yöntem 1 ile aynı şekilde gerçekleştirilmektedir.
İpucu 5: Bir noktanın bir düzlemdeki izdüşümü nasıl bulunur?
Projeksiyon yöntemi inşaat teorisinin temelini oluştururmühendislik grafiklerindeki resimlerin çizimi. Çoğunlukla, vücut görüntüsünü uçak üzerindeki projeksiyon biçiminde bulmak ya da uzaydaki konumu hakkında veri edinmek gerektiğinde kullanılır.

talimat
1
Çok boyutlu bir alanda, herhangi bir görüntüDüzlemdeki nesne projeksiyon ile elde edilebilir. Bununla birlikte, vücut geometrik formunu veya en basit görüntü biçimini bir projeksiyon temelinde geometride değerlendirmemeliyiz nokta. Bir geometrik cisim görüntüsü ile ilgili en eksiksiz bilgi puanların birkaç projeksiyonunu verir. Bu amaçla, vücut noktalarının projeksiyonları en az iki düzlemde kullanılır.
2
Örneğin, projeksiyon nokta A. Bunu yapmak için, iki düzlemi birbirine dik olacak şekilde düzenleyin. Bir yatay olarak, onu yatay olarak adlandır düzlem ve indeks 1 ile elemanların tüm projeksiyonlarını belirtir. İkincisi dikeydir. Sırasıyla frontal olarak isimlendirin. düzlemve elemanların projeksiyonlarını indeks 2'ye atayacaktır. Bu uçaklardan her ikisi de sonsuz ve opak olarak kabul edilir. Koordinat ekseni OX, kesişim çizgileri olur.
3
Sonra projeksiyon düzlemleri arasındaki boşluğun koşullu olarak çeyrek bölünmüş olması gerçeğini kabul edin. İlk çeyrekte bulunuyorsunuz ve yalnızca bu satırları görüyorsunuz ve nokta, dihedral açıdaki bu bölgede bulunmaktadır.
4
İzdüşüm sürecinin özü, ışın verilen bir noktadan kirişi, ışın karşılayana kadar tutmaktır. düzlem projeksiyonlar. Bu yönteme ortogonal projeksiyon metodu denir. Ona göre, atla nokta A, yatay ve ön düzleme dik. Bu dikmenin temeli yalnızca yatay çıkıntıdır nokta A1 veya ön projeksiyon nokta A2. Yani bu pozisyonu aldın nokta verilen projeksiyon düzlemi uzayında.
İpucu 6: Projeksiyon nasıl bulunur?
Dikdörtgen bir üçgende iki tip yan vardır - "kateter" in kısa yanı ve "hipotenürün" uzun tarafı. Eğer devam edersek projeksiyon hipotenüs üzerindeki bacak, iki bölüme ayrılır. Bunlardan birinin değerini belirlemek için, bir girdi veri seti hazırlamanız gerekir.

talimat
1
Sorunun başlangıç verisinde reçete edilebilirProjeksiyonun bulunacağı hipotenüs D uzunluğu ve bacağın uzunluğu. Yansıtma boyutu Nd'yi belirlemek için, bir doğru üçgenin özelliklerini kullanın. Bacağın uzunluğunu, hipotenüsün uzunluğundan ve bacağın izdüşümünden alınan geometrik ortalamanın bacağın istenen boyutuna eşit olması gerçeğini kullanarak belirleyin. Yani, N = √ (D * Nd).
2
Ürünün kökünün o zaman anlamına geldiği göz önüne alındığındageometrik ortalama ile aynı, N değerini sıkıştırın (istenen bacağın uzunluğu) ve hipotenürün uzunluğuna bölün. Nd = (N / √ D) ² = N² / D. Sorunun başlangıç verisinde, uzunluklara yalnızca N ve T bacaklarından verilen değerler verilebilir. Bu durumda, Nd projeksiyonunun uzunluğu Pisagor teoremi kullanılarak bulunmuştur.
3
Projeksiyonu bulmak için hipotenüs D'nin uzunluğunu √ (N² + T²) umbilical değerleri kullanarak belirleyin ve elde edilen değeri formülün yerine koyun. Nd = N² / √ (N² + T²) için.
4
Orijinal veri, bacak Rd'sinin ve hipotenüs D'nin izdüşümünün uzunluğu hakkında bilgi içeriyorsa, en basit çıkarma formülünü kullanarak ikinci ayağın Nd projeksiyon uzunluğunu hesaplayın - Nd = D - Rd.
5
Yalnızca hipotenüs D'nin uzunluğu bilinmekte ve bacaklardaki uzunlukların basit bir oranı verildiği durumda (m / h), ilk adımdaki formüllere ve yardım için üçüncü adıma bakınız.
6
İlk adımdaki formüle göre,Nd ve Rd projeksiyonlarının oranının, uzunluklarının kare değerlerinin oranına denk olması. Yani, Nd / Rd = m² / h²'dir. Ayrıca, bacaklardaki Nd ve Rd projeksiyonlarının toplamı, hipotenürün uzunluğuna eşittir.
7
Rd projeksiyonunun projeksiyonunuİstenen Nd sınıfını bulun ve toplama formülü ile değiştirin. Sonuç olarak, Nd + Nd * m² / h² = Nd * (1 + m2 / h²) = D elde edersiniz ve daha sonra bulma formülünü elde edebilirsiniz Nd = D / (1 + m2 / h²). Nd değeri istenen bacağın boyutunu gösterecektir.
İpucu 7: Bir vektöre ait projeksiyon nasıl belirlenir?
Bir vektör, sıralı bir çift olarak kabul edilebilirUzayda noktalar veya yönlendirilmiş bir bölüm. Analitik geometrinin okul dersinde, projeksiyonlarını - koordinat eksenlerinde, düz bir çizgide, düzlemde veya başka bir vektör üzerinde - belirlemek için genellikle farklı problemler düşünülür. Genellikle, bir vektörün iki ve üç boyutlu dikdörtgen koordinat sistemleri ve dikey projeksiyonları sorundur.

talimat
1
Vektör vektör, başlangıçtaki koordinatlarla verilirseA (X₁, Y₁, Z₁) ve son B noktaları (X₂, Y₂, Z₂) ve bu bulgu, çok basit, koordinat sisteminin dikdörtgen ekseninde çıkıntı (p) gerektirir. İki pozisyondaki ilgili koordinatların farkını hesaplayın - ör. Pz = Z₂-Z₁ - apsis üzerinde çıkıntı vektörü AB Px = X₂-X₁, Py = Y₂-Y₁, z ekseni ordinat eşittir.
2
Bir çift veya üçlü verilen bir vektör için (in{X, Y} veya ā {X, Y, Z} koordinatlarının boşluğun boyutuna bağlı olarak) önceki adımın formüllerini basitleştirin. Bu durumda, koordinat eksenlerine (āx, āy, âz) yaptığı projeksiyonlar karşılık gelen koordinatlara eşittir: ξ = X, āy = Y ve âz = Z.
3
Sorunun koşullarında yöneltilen koordinatlarhiçbir bölüm belirtilmemiştir, ancak uzunluğu verilmiştir | ā | ve cos (x), cos (y), cos (z) yönleri, olağan dikdörtgen üçgende olduğu gibi projeksiyonları koordinat eksenlerine (āx, āy, âz) tanımlar. Sadece uzunluğu ilgili kosinüs ile çarpın: āx = | ā | * cos (x), āy = | ā | * cos (y) ve âz = | ā | * cos (z).
4
Önceki adıma benzer şekilde, vektörün izdüşümüà (X1, Y1) başka bir vektör (X2, Y2) 'ye çevirirken, projeksiyonunu, vektöre paralel ve yönü ona rastlayan bir keyfi olarak alınan bir eksene göre düşünebiliriz. Bu değeri (ā0) hesaplamak için, vektörün modülünü, yöneltilmiş bölümler arasındaki eşitlik (α) ile çarpın. Ā ve ō: = | ā | * cos (α).
5
| O | ā₀ = â * o /: vektörlerin à (X₁, Y₁) ve O (X₂, Y₂) arasındaki açı (ā₀) A o modülünü kendi iç ürünü paylaşmak için projeksiyonlar hesaplanması için, bilinmiyorsa.
6
AB vektörünün dikey olarak L çizgisi üzerine çıkıntısıBu çizginin, orijinal vektörün başlangıç ve son noktalarının dikey projeksiyonlarla oluşturduğu kesimine denir. çizgi açıklayan aşağıdaki formül kullanılarak izdüşümü koordinatlarını belirlemek için (genel olarak * X, + b * Y + C = 0), ve ilk bir (X₁, Y₁) ve vektör noktaları son B (X₂, Y₂) koordinatları.
7
Benzer şekilde, ortogonalvektörün denklemle verilen düzlem üzerindeki izdüşümü - bu, düzlemin iki noktası arasındaki yönlendirilmiş bir segment olmalıdır. Başlangıç noktasının koordinatları, bir düzlemin formülünden ve başlangıç vektörünün başlangıç noktalarının koordinatlarından hesaplar. Aynı şey projeksiyonun son noktası için de geçerlidir.
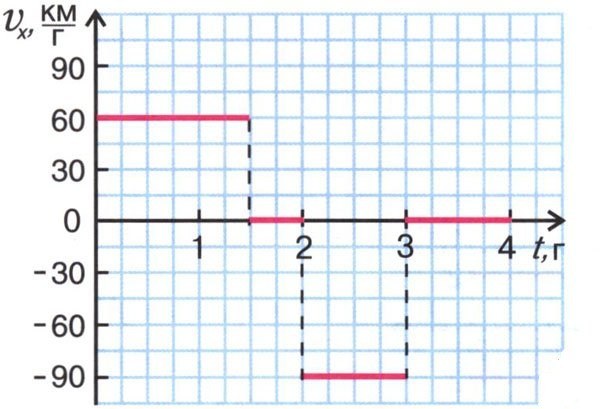
İpucu 8: Sıfır hız nasıl bulunur?
Fizikte, olağan hızın yanı sıra, tanıdıktüm cebir, "sıfır hız" kavramı var. Sıfır hızı veya denildiği gibi, başlangıç hızı, olağan hızı bulmak için kullanılan formülden farklı olarak başka bir şekilde bulunur.

talimat
1
Sıfır hız, çeşitli bilinen yollarla bulunabilir; bunların her biri, bilinen bileşenleri içeren sorunlara uygulanabilir.
2
Sorunun durumunda bir mesafe var ise(S), vücudun hareket ettiği ivme (a) mesafeyi (t) aşması için geçen süreyi (a), sonra sıfır hızını formülünü kullanarak bulur: S = V0t + at ^ 2/2, burada V0 - Sıfır hız, t ^ 2 - t karede. S = 100 m, t = 5 c, a = 2 m / s karede olsun.
3
Sıfır hızını (V0) bulmak içinyukarıda belirtilen formül, bilinmeyen terimi bulma kuralını kullanır: "Bilinmeyen terimi bulmak için, bilinen terimi toplamdan çıkarmanız gerekir." Çıkıyor: V0t = S-at ^ 2/2.
4
Daha sonra bilinmeyen faktörü bulma kuralını uygulayın: "Bilinmeyen faktörü bulmak için, ürünü bilinen çarpana bölün." Çıkıyor: V0 = (S-at ^ 2/2) / t.
5
Elde edilen formülde, bilinen miktarların değerlerini değiştirin. Çıkarsa: V0 = (100-2х5 ^ 2/2) / 5, V0 = (100-25) / 5, V0 = 15 m / sn.
6
Sorunun bulunduğu zaman, verilen uzaklık (S) yerineSıfır hızda (V0) vücut da son hız (V), daha sonra formül kullanılarak V0 bulgu: V = V0 + de burada V - gövdenin son hız ve - zaman - hızlanmasının, hareket parçası, t oranında Vücut hareket ettirilirken. V = 25 m / C, t = 5 c olsun, a = 2 m / c kare.
7
Şimdi, sıfır hızını bulmak içinbilinmeyen terim kuralını kullan. Çıkıyor: V0 = V-at. Bilinen değerleri, elde edilen formüle koyun. Böylece: V0 = 25-2x5, V0 = 25-10, V0 = 15 m / s.







